[논문리뷰] PointCNN: Convolution on X-Transformed Points

[Introduction]

먼저 CNN이 성공할 수 있었던 많은 요인들 중 하나를 본다면 Convolution operator는 Image와 같은 grid에서 공간적인 특징을 추출하는 데에 있어 높은 성능을 보여주었던 점도 포함되겠죠.

하지만 Point cloud에서는 다릅니다. 왜냐하면 Point cloud는 irregular 하고 unordered 하기 때문에 이러한 Point cloud data에 바로 kernel을 적용시킨다는 것은 점의 순서를 다르게 하거나 형상정보를 버리는 꼴이 되니까요.

 

이러한 문제를 다루기 위해 본 논문에서는 학습 가능한 X-transformation을 제안합니다. 이를 통해 convolution은 point cloud의 공간 정보를 얻을 수 있고 unordered 한 point cloud를 canonical order로 만들 수 있게 됩니다.

[X-transformation]

X-transformation을 설명하기 위해 다음 4가지 data를 보겠습니다.

 

Figure 1

Figure 1은 (i) regular grid, (ii~iv) point cloud입니다. 각각의 data는 C-dimensional의 feature를 갖는 unodered set $F=\{f_a,f_b,f_c,f_d\}$이고 4*C의 shape을 갖는 하나의 kernel $K=[k_a,k_b,k_r,k_d]$이 있다고 가정하겠습니다.

그럼 (i)에 convolution연산을 하기 위해서는 $[f_a,f_b,f_c,f_d{]}^T$의 형태로 만들어 kernel K와 연산 $f1=Conv(K,[f_a,f_b,f_c,f_d{]}^T)$를 하면 됩니다. (이때 $Conv(A,B)$는 point-wise product후에 값들을 더하는 것을 의미합니다)

 

Figure 1a

그리고 (ii)~(iv) point cloud 각각에 convolution 연산을 한결과는 Figure 1a와 같습니다.

이때 (ii)와 (iii)의 결과를 보면 (ii)와 (iii)는 분명히 다른 위치의 점들 임에도 불구하고 같은 순서로 입력되었기 때문에 같은 convolution연산 결과를 얻게 됩니다.

반면 (iii)와 (iv)는 같은 위치의 점들 임에도 불구하고 다른 순서로 입력되어 다른 convolution연산 결과를 얻습니다.

결국 Point cloud에 직접 convolution연산을 하는 것은 data의 형상정보를 변형되게 하고 order에 민감한 결과를 초래할 수 있다는 것을 알 수 있습니다.

 

본 논문에서는 위와 같은 문제를 해결하기 위해 K개의 input points들의 좌표를 $X=MLP(p_1,p_2,...,p_k)$를 통해 학습하는 KxK행렬 X-transformation을 제안합니다. X-transformation을 통해 동일한 points이라도 서로 다른 공간에서 다른 가중치를 가질 수 있게 되어 위의 (ii)-(iii)에서의 문제를 해결하고 permutation연산을 통해 order가 재정렬되어 (iii)-(iv)에서의 순서에 의한 민감도 문제를 해결합니다. 이러한 과정을 X-Conv라고 합니다.

 

Figure 1b

Figure 1a에 X-Conv를 적용한 결과는 Figure 1b가 됩니다. 이때 $X_{ii}$와 $X_{iii}$는 각각 다른 shape의 point들을 학습했기에 서로 다를 수 있으며 $X_{iii}$와 $X_{iv}$에서는 permutation연산을 통해 순서를 같도록 합니다.

 

[Hierarchical Convolution]

Figure 2

Regular grid - Figure 2 위의 input은 $F_1=R_1\times R_1\times C_1$( $R_1$=spatial resolution, $C_1$=feature channel) 이고 kernel K의 shape은 $K\times K\times C_1\times C_2$로 convolution의 결과 $F_2=R_2\times R_2\times C_2$를 만듭니다. $F_1$를 기준으로 $F_2$를 보면 lower resolution($R_1$ > $R_2$)이며 deeper channels($C_1$ < $C_2$)이고 더욱 높은 level의 정보를 갖고 있음을 알 수 있습니다.

 

PointCNN - Figure 2 아래의 input은 $F_1=\{(p_{1,i},f_{1,i}):i=1,2,...,N_1\}$ 이고 point들은 $\{p_{1,i}:p_{1,i}\in R^{Dim}\}$이며, feature는 $\{f_{1,i}:f_{1,i}\in R^{C_1}\}$ 입니다. 이후에 X-Conv를 적용시키면 $F_2=\{(p_{2,i},f_{2,i}):i=1,2,...,N_2\}$ 가 되겠죠. Regular grid의 과정과 마찬가지로 smaller spatial resolution $N_2<N_1$, deeper feature channel $C_1<C_2$ 가 됩니다.

 

본 논문은 representation point를 random sampling을 통해 선택하였지만 추가 연구가 필요할 수 있다고 말합니다.

 

[X-Conv Operator]

Algorithm 1

Input은 다음과 같습니다.

$K$ : kernel, $p$ : random sampling된 대표 point, $P$ : 이웃한 unordered point set, $F$ : $P$의 features

 

1. $P$를 $p$를 기준으로한 local 좌표계로 변환하여 $P^{\prime }$을 만듭니다.

$P-p$

2. $P^{\prime }$의 point들의 좌표 각각에 $ML{P}_{\delta }$를 적용하여 $F_{\delta }$를 만듭니다.

(이때 만들어지는 $F_{\delta }$는 Input $F$의 order와 동일합니다)

$ML{P}_{\delta }(P^{\prime })$

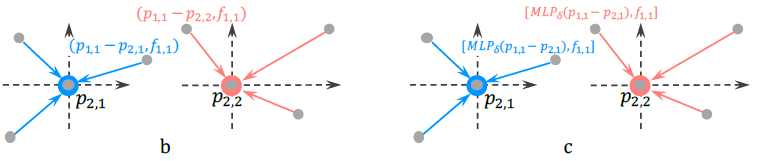
3. $F_{\delta }$와 $F$를 concatenate하여 $K\times (C_{\delta }+C_1)$ shape의 $F_{\ast }$ matrix를 만듭니다.

4. $P^{\prime }$ 전체에 $MLP$를 적용하여 앞서 설명한 $K\times K$ X-transformation matrix를 학습합니다. 

5. $X\times F_{\ast }$를 수행하여 $F_X$를 구합니다.

6. 마지막으로 Conv($K$, $F_X$)를 통해  $K\times (C_{\delta }+C_1)\times C_2$ shape의 $F_p$를 구합니다.

 

[PointCNN Architectures]

Figure 4

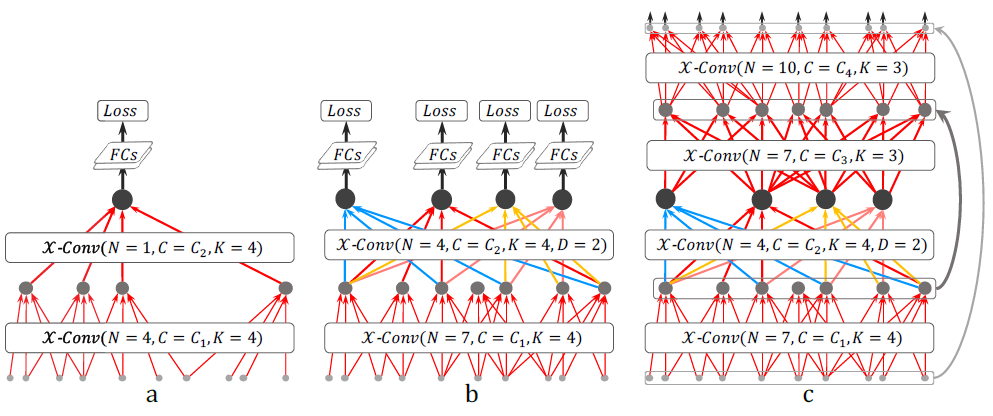
Figure 4a : 두번의 X-Conv layer를 통해 더 많은 특징정보를 담고 있는 representation point를 구합니다. receptive field는 K/N(K : neighboring point number, N : point number in the previous layer)의 비율로 감소합니다. 생성되는 하나의 representation point는 전체 point들의 global view와 형상이 shape의 의미를 위한 feature를 갖고 있습니다. 

-> training sample이 빠르게 감소한다는 단점이 문제가 있다.

 

Figure 4b : network의 depth는 그대로 두고 receptive field만을 늘리고 싶어 grid-based CNN의 hollow convolution의 개념을 도입합니다. 그러면 receptive field를 $K\times D/N$의 비율로 만들 수 있고 더 많은 representation point를 남길 수 있게 됩니다.

 

grid-based CNN의 hollow convolution은 왼쪽의 이미지와 같이 동작하는 convolution 연산을 의미합니다.

 

 

 

 

Figure 4c : segmentation task를 위해선 high resolution point-wise output이 필요합니다. 그래서 본 논문에서는 U-net의 Conv-DeConv(정확히는 Transpose convolution) 구조를 사용합니다. 그럼 point단위로 segmentation을 진행할 수 있겠죠.